How To Understand The Big O Notation: A Guide To Complexity And Efficiency

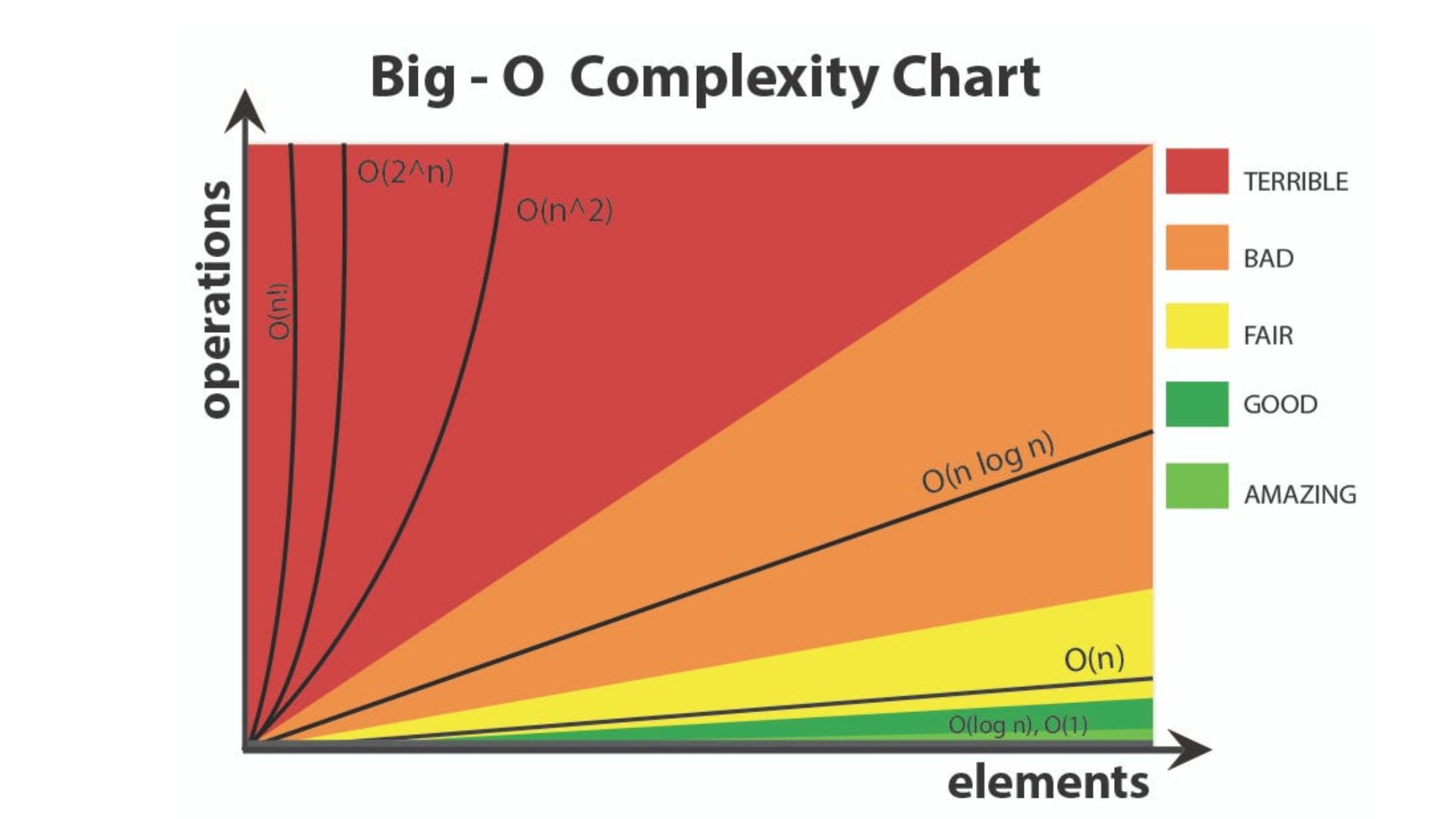
Understanding the Big O Notation is crucial for anyone diving into the realm of algorithms and data structures. It serves as a standardized way to describe the efficiency of an algorithm, helping developers make informed decisions about code optimization. Let's embark on a journey to demystify the Big O Notation and grasp its significance in assessing algorithmic complexity.

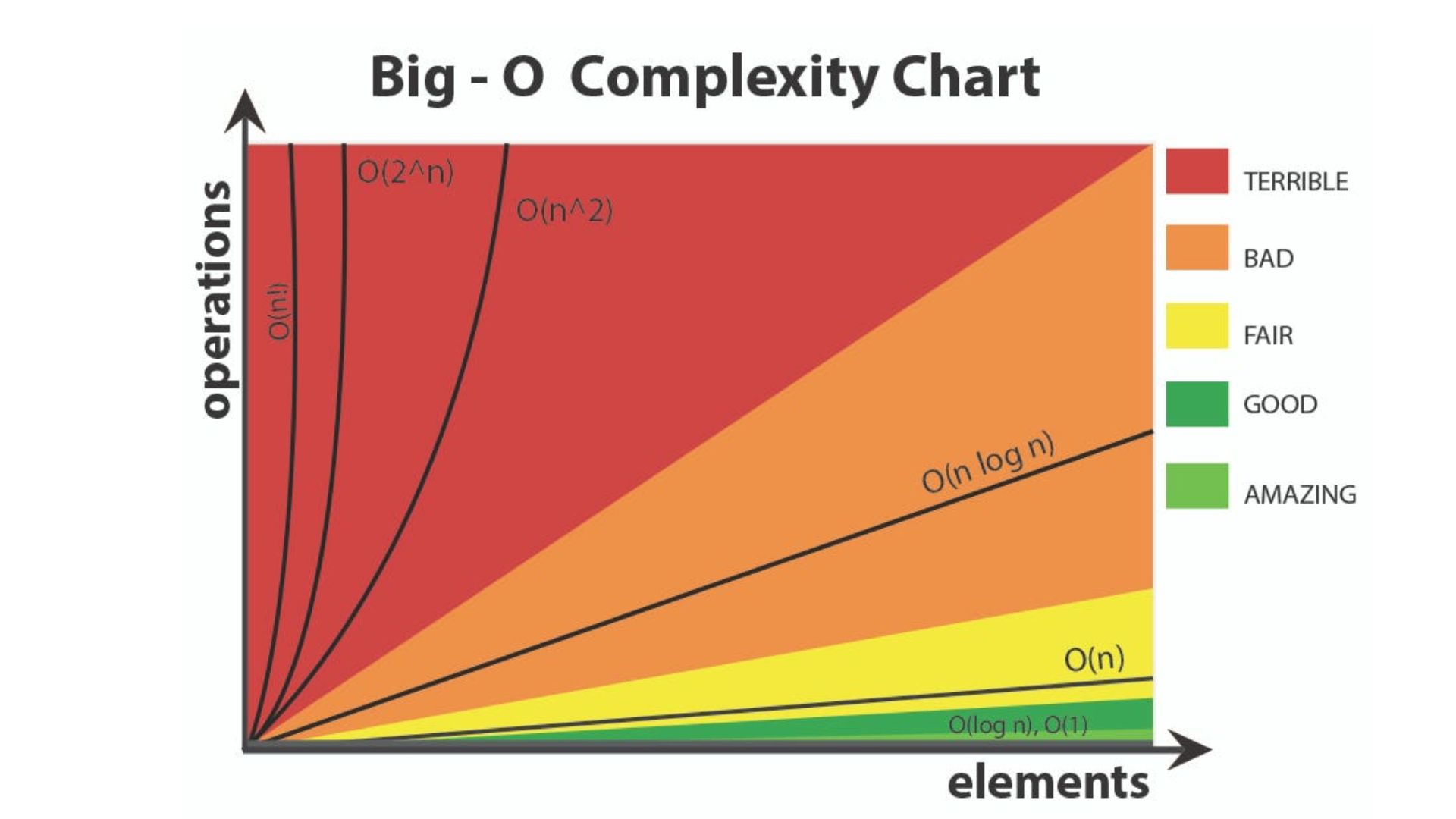
At its core, the Big O Notation provides a simplified representation of an algorithm's performance as the size of the input increases. It quantifies the upper bound or worst-case scenario of an algorithm's time or space complexity. For example, O(1) denotes constant time complexity, O(log n) represents logarithmic complexity, O(n) indicates linear complexity, and so on.

To better comprehend Big O, consider a scenario where you're tasked with searching for a specific element in an unsorted list. A linear search algorithm would have a time complexity of O(n), as the worst-case scenario involves iterating through the entire list. On the other hand, a binary search on a sorted list boasts a time complexity of O(log n) due to its divide-and-conquer approach.

To master Big O Notation, one must familiarize themselves with common time complexities and understand how different operations contribute to an algorithm's overall efficiency. Practice dissecting code snippets and identifying their Big O complexities, and soon you'll find yourself making informed decisions to optimize your code.

In conclusion, the Big O Notation is an invaluable tool for developers striving to write efficient and scalable code. Embrace its principles, practice its application, and watch as your algorithmic prowess grows.